A solid right pyramid has a square base – A solid right pyramid with a square base is a three-dimensional shape with unique geometric properties and practical applications. Its square base and right triangular faces give it distinctive characteristics that set it apart from other types of pyramids. This article explores the geometry, properties, and uses of a solid right pyramid with a square base, providing insights into its mathematical significance and real-world relevance.
The discussion will delve into the characteristics of its square base, the definition and properties of a right pyramid, the number of faces and edges, formulas for calculating volume and surface area, different types of cross-sections, and examples of its applications in architecture, engineering, and design.
Solid Right Pyramid with a Square Base: A Solid Right Pyramid Has A Square Base
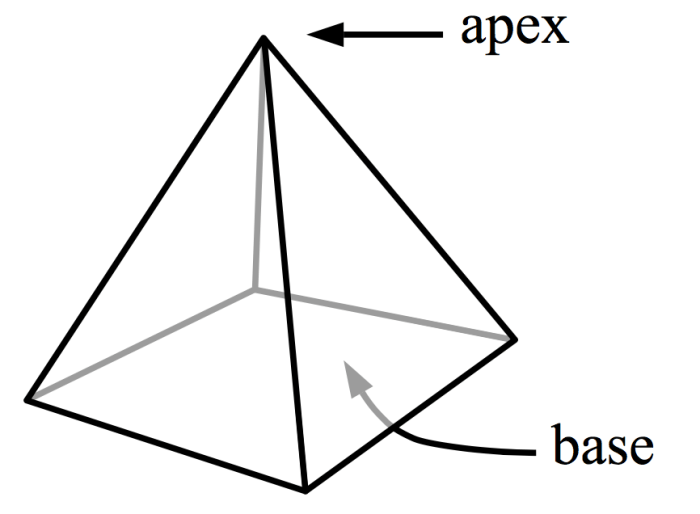
A solid right pyramid with a square base is a three-dimensional shape with a square as its base and four triangular faces that meet at a single vertex.
Square Base
The square base of a solid right pyramid has the following characteristics:
- It is a regular quadrilateral with four equal sides and four right angles.
- The side length of the square is referred to as the “base length” (b) of the pyramid.
The square base serves as the foundation of the pyramid and determines its stability and overall shape.
Right Pyramid, A solid right pyramid has a square base
A right pyramid is a pyramid whose base is a regular polygon and whose apex (vertex) is directly above the center of the base.
The defining characteristics of a right pyramid are:
- It has a regular polygonal base.
- Its lateral faces are triangular and congruent.
- Its apex lies directly above the center of the base.
A solid right pyramid with a square base is a specific type of right pyramid where the base is a square.
Faces and Edges
A solid right pyramid with a square base has the following number of faces and edges:
- Faces:5 (1 square base and 4 triangular faces)
- Edges:8 (4 base edges and 4 lateral edges)
The faces and edges of the pyramid are related as follows:
- Each base edge is shared by two triangular faces.
- Each lateral edge connects the apex to a vertex of the base.
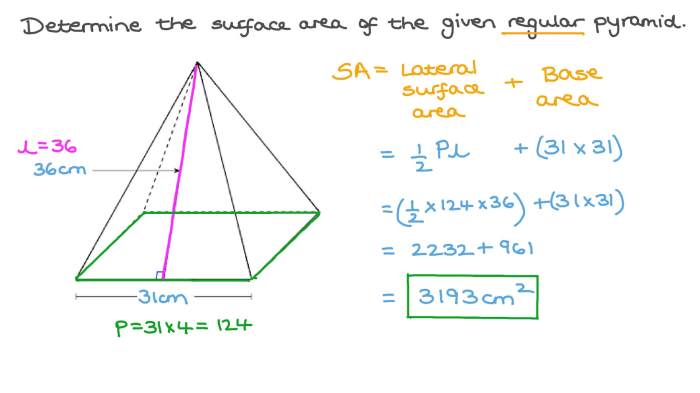
Volume and Surface Area
The volume and surface area of a solid right pyramid with a square base are calculated using the following formulas:
Volume:
V = (1/3)
- b^2
- h
where:
- V is the volume of the pyramid
- b is the length of the base side
- h is the height of the pyramid (distance from the apex to the base)
Surface Area:
A = b^2 + 4
- (1/2)
- b
- √(h^2 + (b/2)^2)
where:
- A is the surface area of the pyramid
- b is the length of the base side
- h is the height of the pyramid
The dimensions of the base and height significantly affect the volume and surface area of the pyramid.
Cross-Sections
When a solid right pyramid with a square base is cut by a plane, the resulting cross-section can vary depending on the angle of the cut.
- Horizontal Cross-Section:If the cut is parallel to the base, the cross-section is a square.
- Vertical Cross-Section:If the cut passes through the apex and a base edge, the cross-section is a triangle.
- Oblique Cross-Section:If the cut is at an angle to both the base and the apex, the cross-section is a trapezoid.
The shape of the cross-section provides insights into the internal structure of the pyramid.
Applications
Solid right pyramids with square bases have various applications in architecture, engineering, and design.
- Architecture:Pyramids have been used for centuries as monumental structures, such as the Egyptian pyramids and the Louvre Pyramid in Paris.
- Engineering:Pyramids can be used as supports or load-bearing structures in bridges, buildings, and other constructions.
- Design:Pyramids can be used as decorative elements in furniture, jewelry, and other objects.
The unique shape and structural properties of solid right pyramids make them suitable for various practical applications.
Helpful Answers
What is the relationship between the base and the other faces of a solid right pyramid with a square base?
The square base is perpendicular to the lateral faces, which are congruent right triangles.
How does the height of a solid right pyramid with a square base affect its volume?
The volume is directly proportional to the height. As the height increases, so does the volume.
What are some real-world applications of solid right pyramids with square bases?
They are used in architecture (e.g., pyramids, roofs), engineering (e.g., bridges, dams), and design (e.g., packaging, sculptures).